[99클럽 코테 스터디 8일차 TIL] DFS와 DP를 사용해 타겟 넘버 문제 풀이

문제

프로그래머스 - 타겟 넘버 문제를 보고 풀이한 내용이다.

n개의 음이 아닌 정수들이 있습니다. 이 정수들을 순서를 바꾸지 않고 적절히 더하거나 빼서 타겟 넘버를 만들려고 합니다. 예를 들어 [1, 1, 1, 1, 1]로 숫자 3을 만들려면 다음 다섯 방법을 쓸 수 있습니다.

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

사용할 수 있는 숫자가 담긴 배열 numbers, 타겟 넘버 target이 매개변수로 주어질 때 숫자를 적절히 더하고 빼서 타겟 넘버를 만드는 방법의 수를 return 하도록 solution 함수를 작성해주세요.

제한사항

• 주어지는 숫자의 개수는 2개 이상 20개 이하입니다.
• 각 숫자는 1 이상 50 이하인 자연수입니다.
• 타겟 넘버는 1 이상 1000 이하인 자연수입니다.

풀이

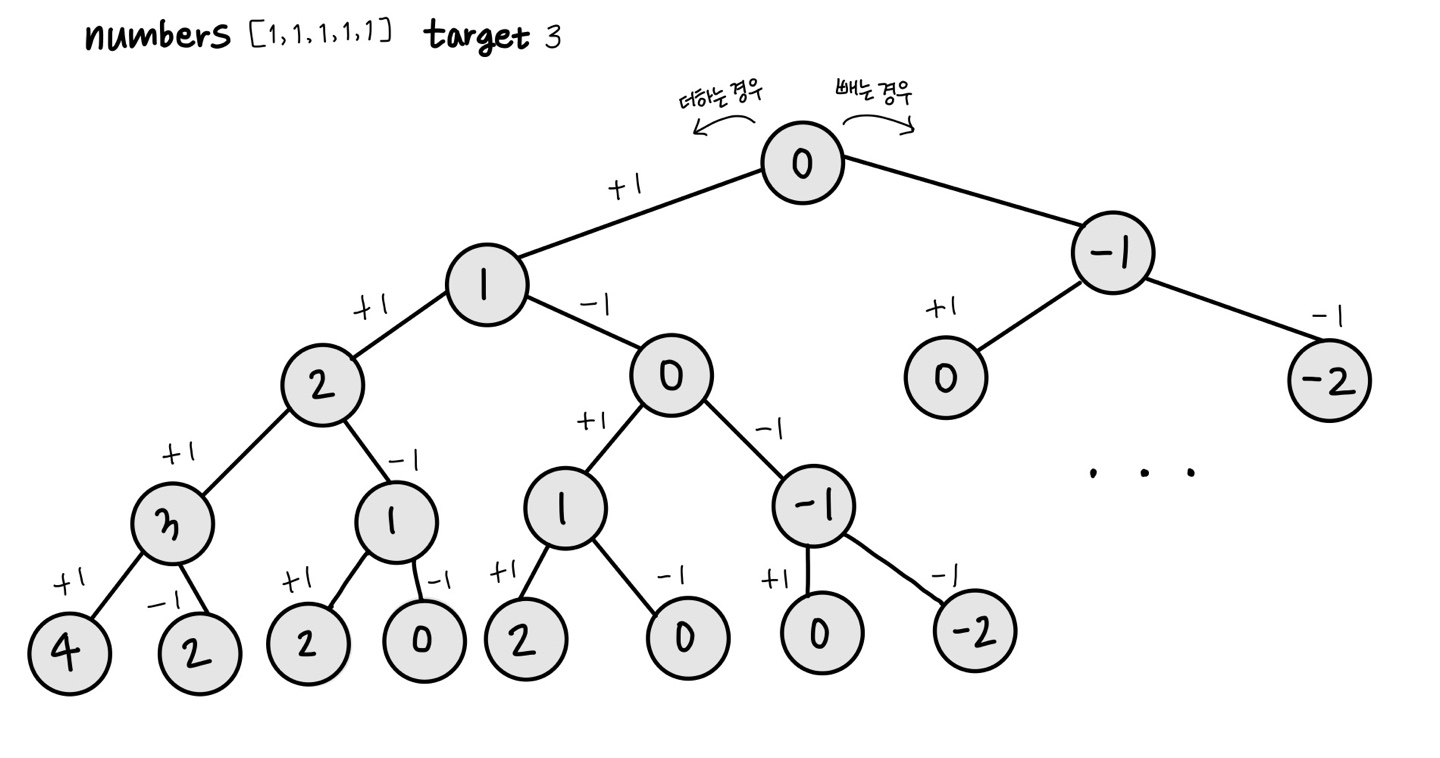
주어진 배열 numbers가 [1, 1, 1, 1, 1]인 경우를 살펴보자.

numbers의 0번째인 1을 선택했다면, 우리가 선택할 수 있는 경우는 다음과 같다.

1. 다음 숫자를 더한다.
2. 다음 숫자를 뺀다.

그렇다면, 현재 숫자에 다음 숫자를 더한 경우와 현재 숫자에 다음 숫자를 뺀 경우를 모두 구해 해당 숫자가 타겟 넘버를 만족하는 경우를 추려내면 정답을 구할 수 있을 것이다.

왜 DFS를 사용해야 할까?

모든 경우의 수 탐색

DFS는 모든 가능한 경우를 탐색하는 데 유용하다. 각 단계마다 선택할 수 있는 모든 옵션을 고려하면서 깊이 우선으로 탐색하기 때문에 가능한 모든 경우의 수를 탐색할 수 있다.

재귀 호출을 통한 문제 분할

위 문제는 문제를 작은 부분 문제로 나누어 해결할 수 있다. 각 단계에서는 현재 숫자를 선택하거나 선택하지 않는 두 가지 선택지가 있기 때문에 재귀 호출을 사용하여 이런 선택을 하나씩 따라가면서 문제를 해결할 수 있다.

탐색 공간 절약

DFS는 불필요한 탐색을 줄일 수 있다. 에를 들어, 탐색 중에 이미 타겟 넘버를 만들 수 없는 경우는 탐색할 필요가 없으므로 해당 경로를 중지할 수 있다.

// 모든 숫자를 사용한 경우 현재까지의 합이 타겟 넘버와 같은지 확인
if (currentSum == target) {
    return 1;
} else {
    return 0;
}

위 코드가 그 역할을 수행한다.

현재까지의 합이 타겟 넘버와 같은지 확인하고 만약 같다면 경우의 수를 1로 반환한다. 이 경우는 더 이상 해당 경로를 탐색하지 않는다.

만약 현재까지의 합이 타겟 넘버와 같지 않다면 다음 단계로 넘어가서 숫자를 더하거나 빼는 경우를 탐색하게 된다.

DFS - 정답 코드

public int solution(int[] numbers, int target) {
        return dfs(numbers, target, 0, 0);
    }

    public int dfs(int[] numbers, int target, int index, int currentSum) {
        // 모든 숫자를 사용한 경우
        if (index == numbers.length) {
            // 현재까지의 합이 타겟 넘버와 같은지 확인
            if (currentSum == target) {
                return 1;
            } else {
                return 0;
            }
        } else {
            // 현재 숫자를 더하는 경우와 빼는 경우 각각에 대해 DFS 호출
            return dfs(numbers, target, index + 1, currentSum + numbers[index]) +
                    dfs(numbers, target, index + 1, currentSum - numbers[index]);
        }
    }

시간 복잡도

DFS를 사용해 문제를 해결한다면 각 단계마다 두 가지 선택지가 있으므로 재귀 호출이 O(2^N)번 일어날 수 있다. 이는 숫자가 커질수록 비효율적인 알고리즘이 된다. 더 효율적으로 개선할 수는 없을까?

Dynamic Programming으로 시간 복잡도 개선하기

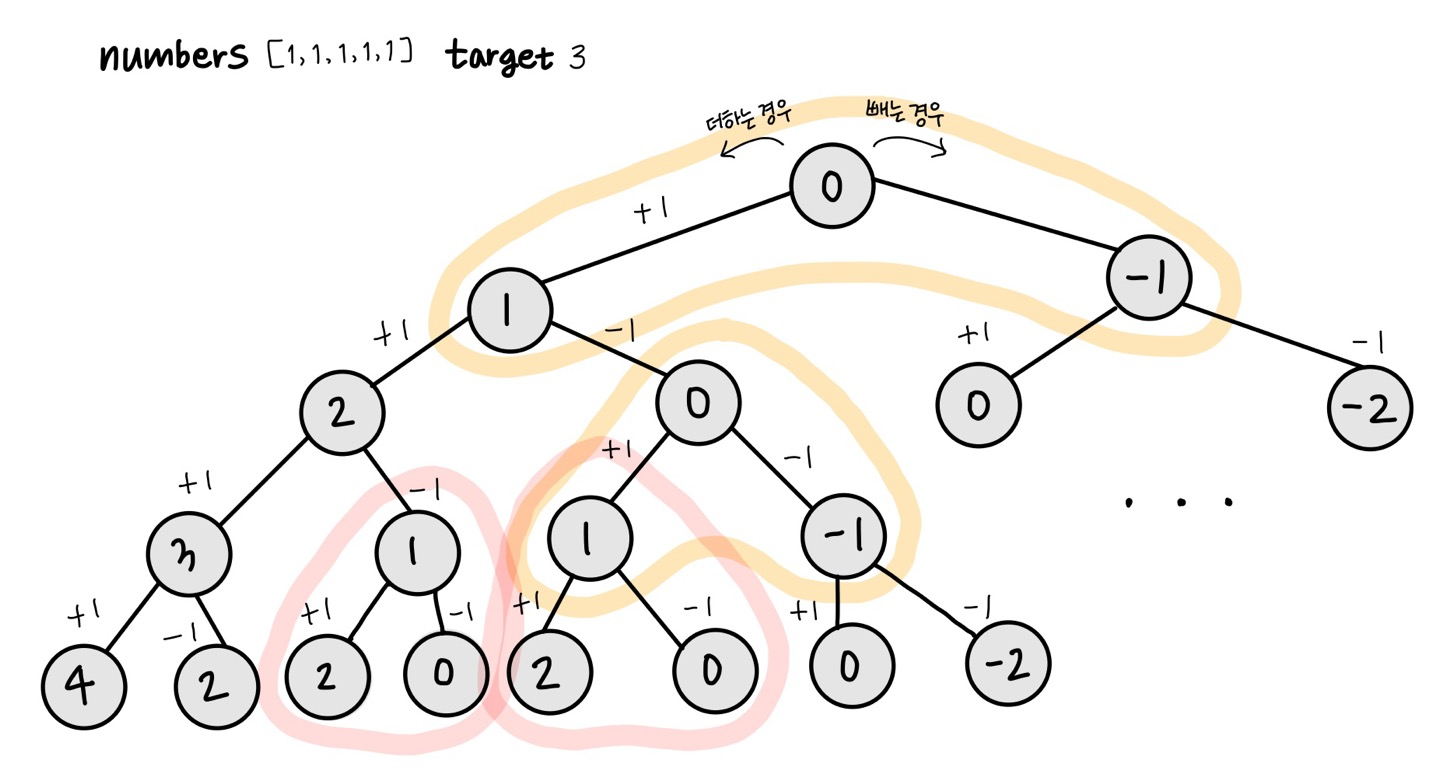
아까 보았던 그림을 다시 살펴보자. 중복되는 부분이 보인다.

현재까지의 합계가 0이라면, 더하는 경우를 선택했을 때의 하위 트리와 빼는 경우를 선택했을 때의 하위 트리는 동일한 구조를 가진다.

이미 계산한 값에 대한 결과를 저장해두어 중복되는 계산을 없앤다면 O(N×M)의 시간 복잡도로 문제를 해결할 수 있다.

DP - 정답 코드

public int solution(int[] numbers, int target) {
        return dfs(numbers, target, 0, 0, new Integer[numbers.length][2001]);
    }

    public int dfs(int[] numbers, int target, int index, int currentSum, Integer[][] memo) {
        if (index == numbers.length) {
            // 모든 숫자를 사용한 경우 현재까지의 합이 타겟 넘버와 같은지 확인
            if (currentSum == target) {
                return 1;
            } else {
                return 0;
            }
        }
        
        // 이미 계산한 값이 있는 경우 해당 값 반환
        if (memo[index][currentSum + 1000] != null) {
            return memo[index][currentSum + 1000];
        }
        
        // 현재 숫자를 더하는 경우와 빼는 경우 각각에 대해 재귀 호출하여 모든 조합 확인
        int count = 0;
        count += dfs(numbers, target, index + 1, currentSum + numbers[index], memo);
        count += dfs(numbers, target, index + 1, currentSum - numbers[index], memo);
        
        // 계산한 값 메모이제이션
        memo[index][currentSum + 1000] = count;
        return count;
    }