[99클럽 코테 스터디 9일차 TIL] BFS를 사용해 게임 맵 최단 거리 문제 풀이
문제
프로그래머스 - 게임 맵 최단 거리 문제를 보고 풀이한 내용이다.
ROR 게임은 두 팀으로 나누어서 진행하며, 상대 팀 진영을 먼저 파괴하면 이기는 게임입니다. 따라서, 각 팀은 상대 팀 진영에 최대한 빨리 도착하는 것이 유리합니다.
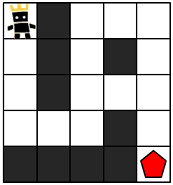
지금부터 당신은 한 팀의 팀원이 되어 게임을 진행하려고 합니다. 다음은 5 x 5 크기의 맵에, 당신의 캐릭터가 (행: 1, 열: 1) 위치에 있고, 상대 팀 진영은 (행: 5, 열: 5) 위치에 있는 경우의 예시입니다.
위 그림에서 검은색 부분은 벽으로 막혀있어 갈 수 없는 길이며, 흰색 부분은 갈 수 있는 길입니다. 캐릭터가 움직일 때는 동, 서, 남, 북 방향으로 한 칸씩 이동하며, 게임 맵을 벗어난 길은 갈 수 없습니다. 아래 예시는 캐릭터가 상대 팀 진영으로 가는 두 가지 방법을 나타내고 있습니다.
첫 번째 방법은 11개의 칸을 지나서 상대 팀 진영에 도착했습니다.
두 번째 방법은 15개의 칸을 지나서 상대팀 진영에 도착했습니다.
위 예시에서는 첫 번째 방법보다 더 빠르게 상대팀 진영에 도착하는 방법은 없으므로, 이 방법이 상대 팀 진영으로 가는 가장 빠른 방법입니다.
만약, 상대 팀이 자신의 팀 진영 주위에 벽을 세워두었다면 상대 팀 진영에 도착하지 못할 수도 있습니다. 예를 들어, 다음과 같은 경우에 당신의 캐릭터는 상대 팀 진영에 도착할 수 없습니다.
게임 맵의 상태 maps가 매개변수로 주어질 때, 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값을 return 하도록 solution 함수를 완성해주세요. 단, 상대 팀 진영에 도착할 수 없을 때는 -1을 return 해주세요.
제한사항
maps는 n x m 크기의 게임 맵의 상태가 들어있는 2차원 배열로, n과 m은 각각 1 이상 100 이하의 자연수입니다.- n과 m은 서로 같을 수도, 다를 수도 있지만, n과 m이 모두 1인 경우는 입력으로 주어지지 않습니다.
maps는 0과 1로만 이루어져 있으며, 0은 벽이 있는 자리, 1은 벽이 없는 자리를 나타냅니다. 처음에 캐릭터는 게임 맵의 좌측 상단인 (1, 1) 위치에 있으며, 상대방 진영은 게임 맵의 우측 하단인 (n, m) 위치에 있습니다.
풀이
maps로 [[1,0,1,1,1],[1,0,1,0,1],[1,0,1,1,1],[1,1,1,0,1],[0,0,0,0,1]] 이 주어진 경우를 그림으로 그려보자.
1
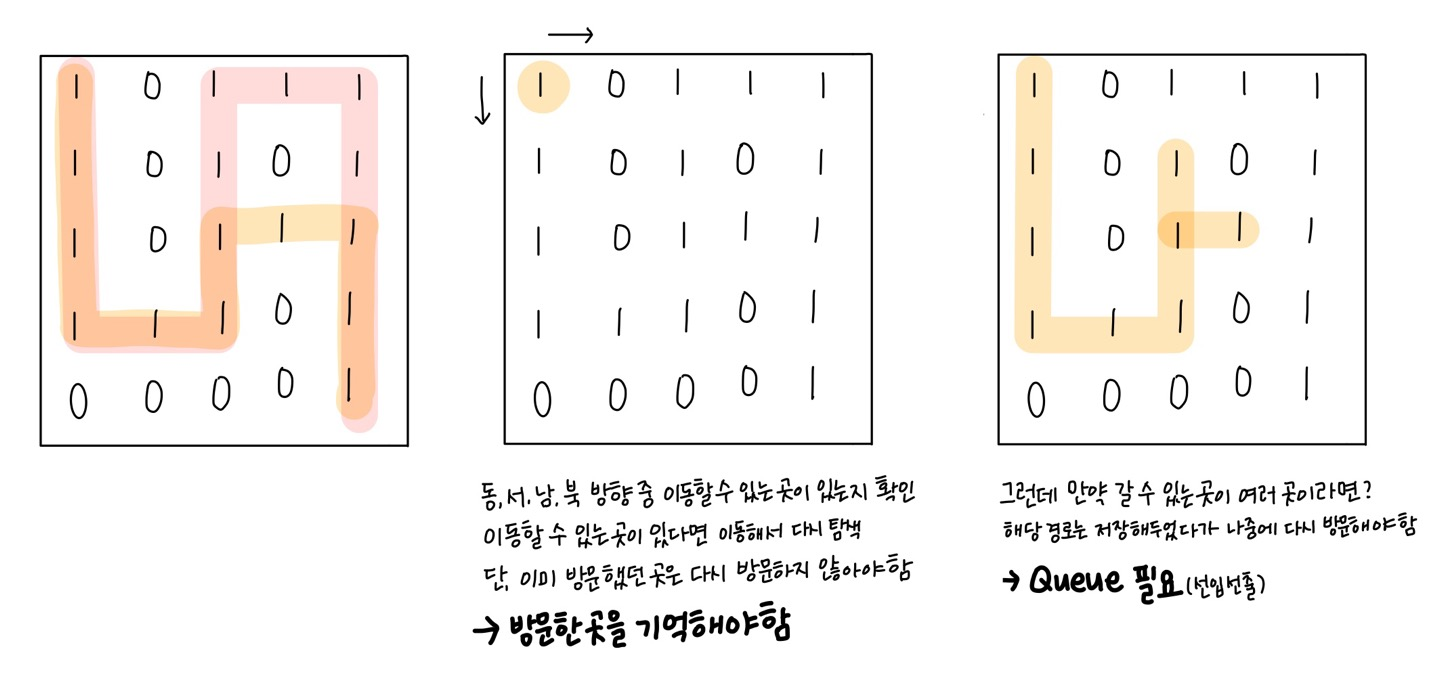
동, 서, 남, 북 방향 중 이동할 수 있는 곳이 있는지(1인 경우) 확인하고 이동할 수 있는 곳이 있다면 이동한다.
위 과정을 계속 반복하면 첫 번째 그림과 같은 경로를 얻을 수 있다.
그런데 주의할 점이 있다. 만약 이미 방문했던 곳을 기억해두지 않는다면 프로그램은 계속해서 같은 경로를 맴돌고 무한 루프에 빠지게 될 것이다.
따라서 방문한 곳을 기억해 둘 공간이 필요하다.
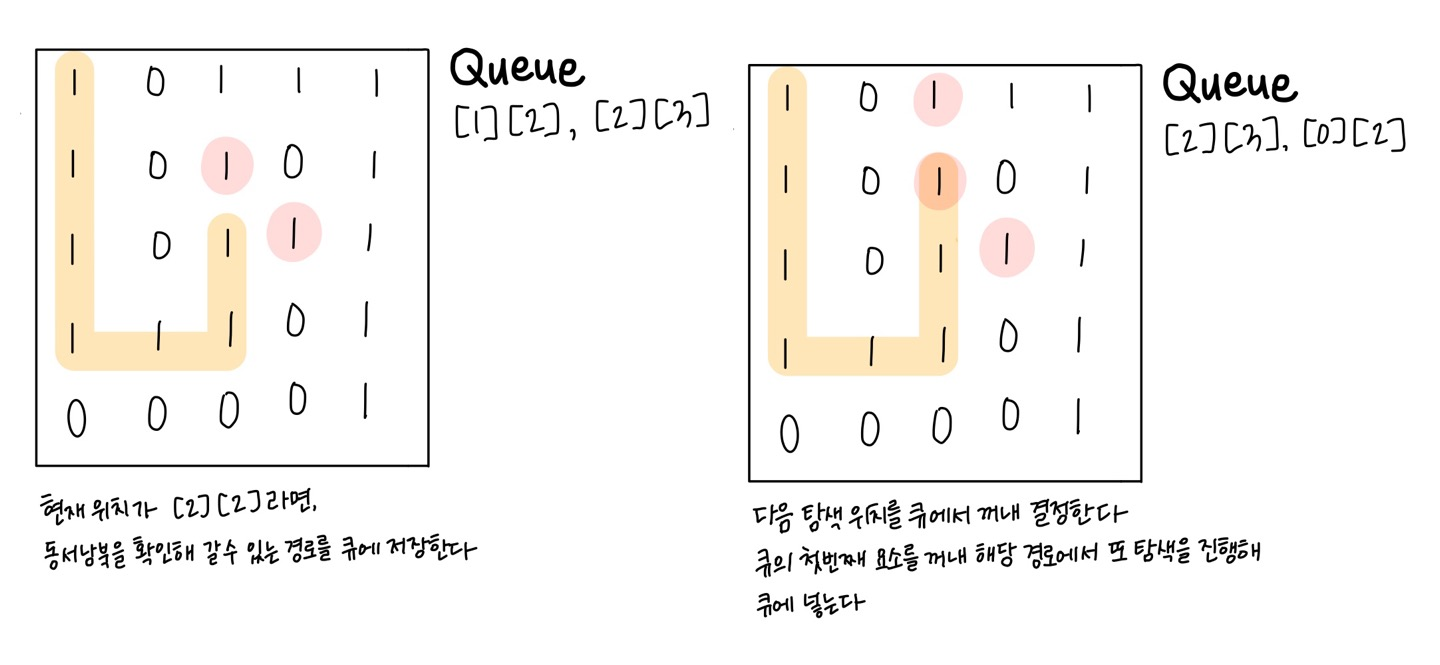
또, 세 번째 그림과 같은 경우를 생각해보아야 한다. 문제에 따르면 캐릭터가 이동할 수 있는 경로는 여러 가지가 나올 수 있기 때문에 수 많은 갈림길을 선택해야 한다. 선택되지 못한 갈림길을 왔던 길 처음부터 다시 탐색하는 일은 너무 비효율적이다.
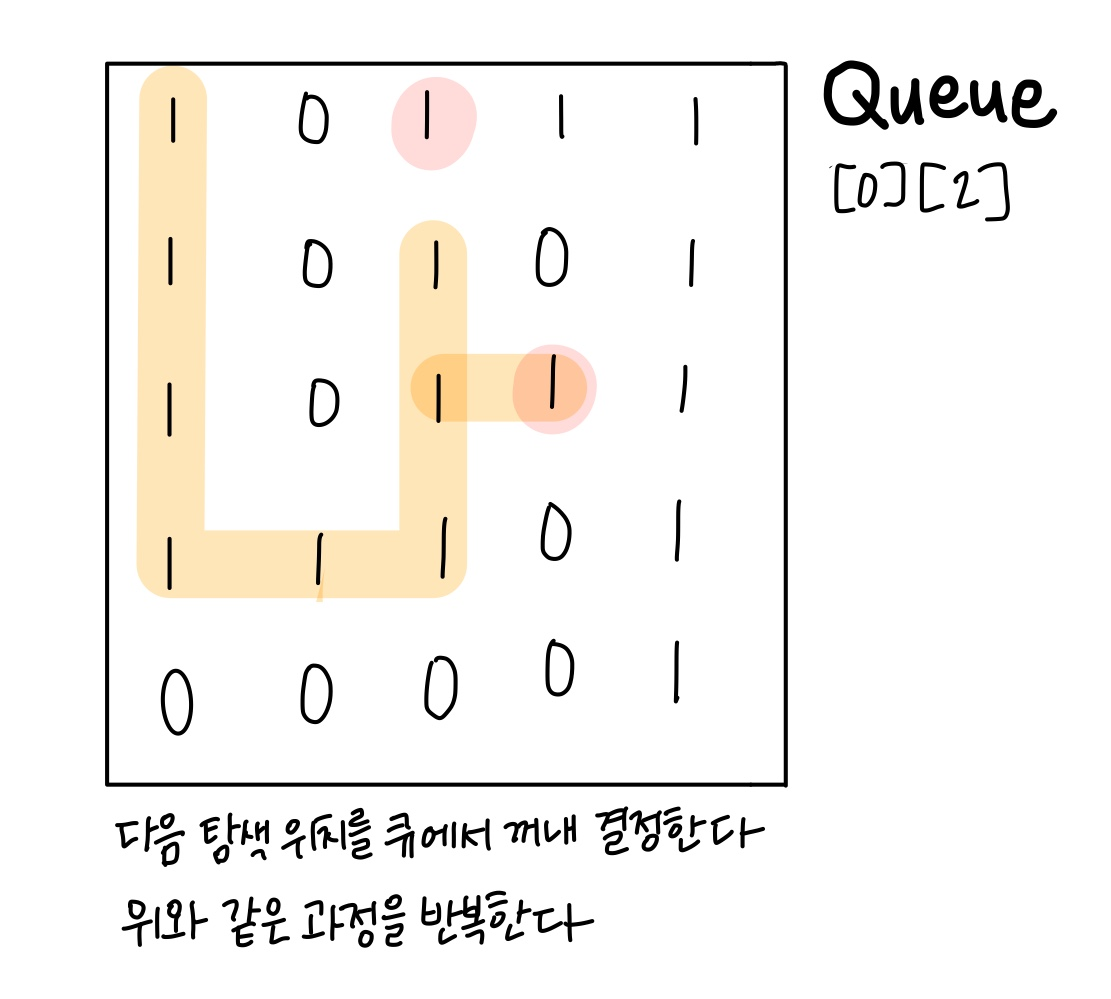
현재 위치에서 이동할 수 있는 경로를 기억해 두었다가 해당 위치에서 이동할 수 있는 최단 거리를 계속해서 선택해 나가면 결국 전체 경로의 최단 경로까지 구해낼 수 있을 것이다.
이런 방법을 BFS(Breadth First Search; 너비 우선 탐색) 이라고 한다.
BFS의 장점
이 문제에서 BFS를 사용해야 하는 이유와 얻을 수 있는 장점에 대해 알아보자.
최단 경로 탐색
BFS는 시작 지점으로부터 가까운 정점부터 방문하기 때문에, 목표 지점에 도착하는 경로 중에서 최단 경로를 보장한다. 위 문제에서 캐릭터가 상대 팀 진영에 도착하기 위해서 지나가야 하는 칸의 개수의 최솟값을 요구하고 있기 때문에 BFS를 사용하기에 적합하다.
가중치가 없는 그래프
문제는 벽(0)과 길(1)로만 이루어진 그래프며 모든 간선의 가중치가 동일하다. 이런 경우는 BFS가 최단 경로를 찾기에 적합하다. 만약 가중치가 있다면 BFS가 최단 경로를 보장하지 않기 때문에 다익스트라와 같은 알고리즘이 더 적합할 수 있다.
시간 복잡도
완전 탐색으로 푸는 경우
이 문제를 완전 탐색으로 푼다고 생각해보자. 모든 가능한 경로를 탐색하여 최단 경로를 찾아야 한다. 이럴 경우 시간 복잡도는 최악의 경우 맵의 크기에 따라 지수적으로 증가한다. 즉 O(2^(n*m))이 된다.
BFS로 푸는 경우
BFS로 문제를 해결하면 시작 지점에서부터 너비 우선으로 탐색을 진행한다. BFS의 특성상 같은 레벨에 있는 모든 정점을 한 번에 처리하므로 최단 경로를 보장한다. 따라서 BFS의 시간 복잡도는 O(V + E)가 된다. V는 정점의 수이고, E는 간선의 수이다. 이 문제에서는 맵의 크기에 비례하여 정점의 수와 간선의 수가 결정되므로 시간 복잡도는 O(n*m)이 된다.
정답 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public class GameMapShortDistance {
// 상, 하, 좌, 우
int[] dx = {0, 0, -1, 1};
int[] dy = {1, -1, 0, 0};
public int solution(int[][] maps) {
int answer = 0;
// 방문한 곳을 기억할 배열
int[][] visited = new int[maps.length][maps[0].length];
// BFS 수행
bfs(maps, visited);
answer = visited[maps.length - 1][maps[0].length - 1];
return answer == 0 ? -1 : answer;
}
public void bfs(int[][] maps, int[][] visited) {
int x = 0;
int y = 0;
// 처음 캐릭터는 (1, 1)에서 시작
visited[x][y] = 1;
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{x, y});
// 큐가 비어있지 않은 동안
while (!queue.isEmpty()) {
int[] current = queue.remove();
int cX = current[0];
int cY = current[1];
// 상하좌우를 탐색
for (int i = 0; i < 4; i++) {
int nX = cX + dx[i];
int nY = cY + dy[i];
// 만약 map의 범위를 벗어나는 경우 다음 탐색으로 건너뜀
if (nX < 0 || nX > maps.length - 1 || nY < 0 || nY > maps[0].length - 1)
continue;
// 아직 방문하지 않은 곳이고, 벽이 없는 자리라면 방문한 뒤 queue에 추가한다
if (visited[nX][nY] == 0 && maps[nX][nY] == 1) {
visited[nX][nY] = visited[cX][cY] + 1;
queue.add(new int[]{nX, nY});
}
}
}
}
}