[99클럽 코테 스터디 10일차 TIL] DFS/BFS를 사용해 Deepest Leaves Sum 문제 풀이
문제
Leetcode - Deepest Leaves Sum 문제를 보고 풀이한 내용이다.
Given the root of a binary tree, return the sum of values of its deepest leaves.
Example 1:
Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8] Output: 15
Example 2:
Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5] Output: 19
풀이
처음엔 단순하게 가장 깊은 위치에 있는 노드를 찾아내기 위해 깊이 우선 탐색 방법을 선택해서 풀었다.
Example 1의 예시를 이용해 탐색을 시작해보자.
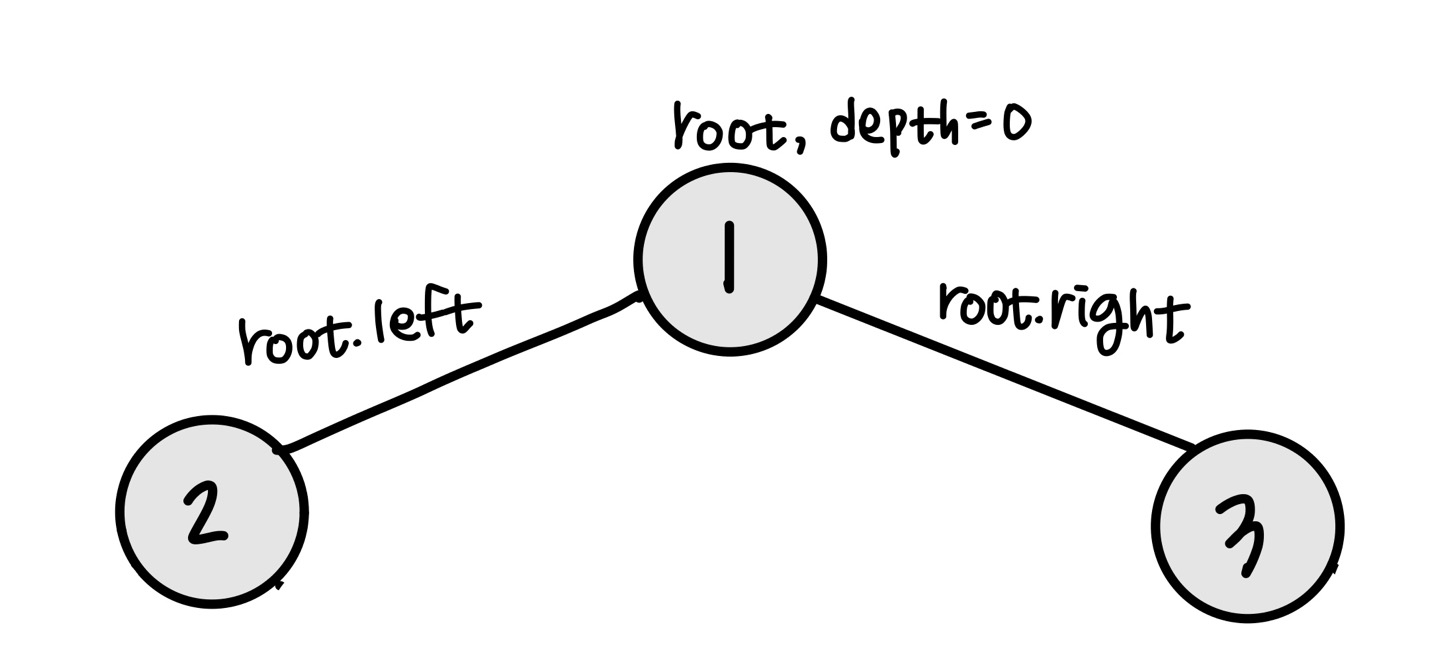
루트 노드 1에서 탐색을 시작한다. 탐색은 다음과 같은 절차를 따른다.
1
2
3
1. 현재 깊이와 가장 큰 깊이를 비교하고, 만약 현재 깊이가 더 크면 가장 큰 깊이를 갱신한다.
2. 가장 큰 깊이의 값을 저장해둔다. 이후에 또 다른 가장 큰 깊이의 값을 구하면 더해주어야 하기 때문이다!
3. 현재 깊이와 가장 큰 깊이가 같다면 저장된 값에 현재 값을 더한다.
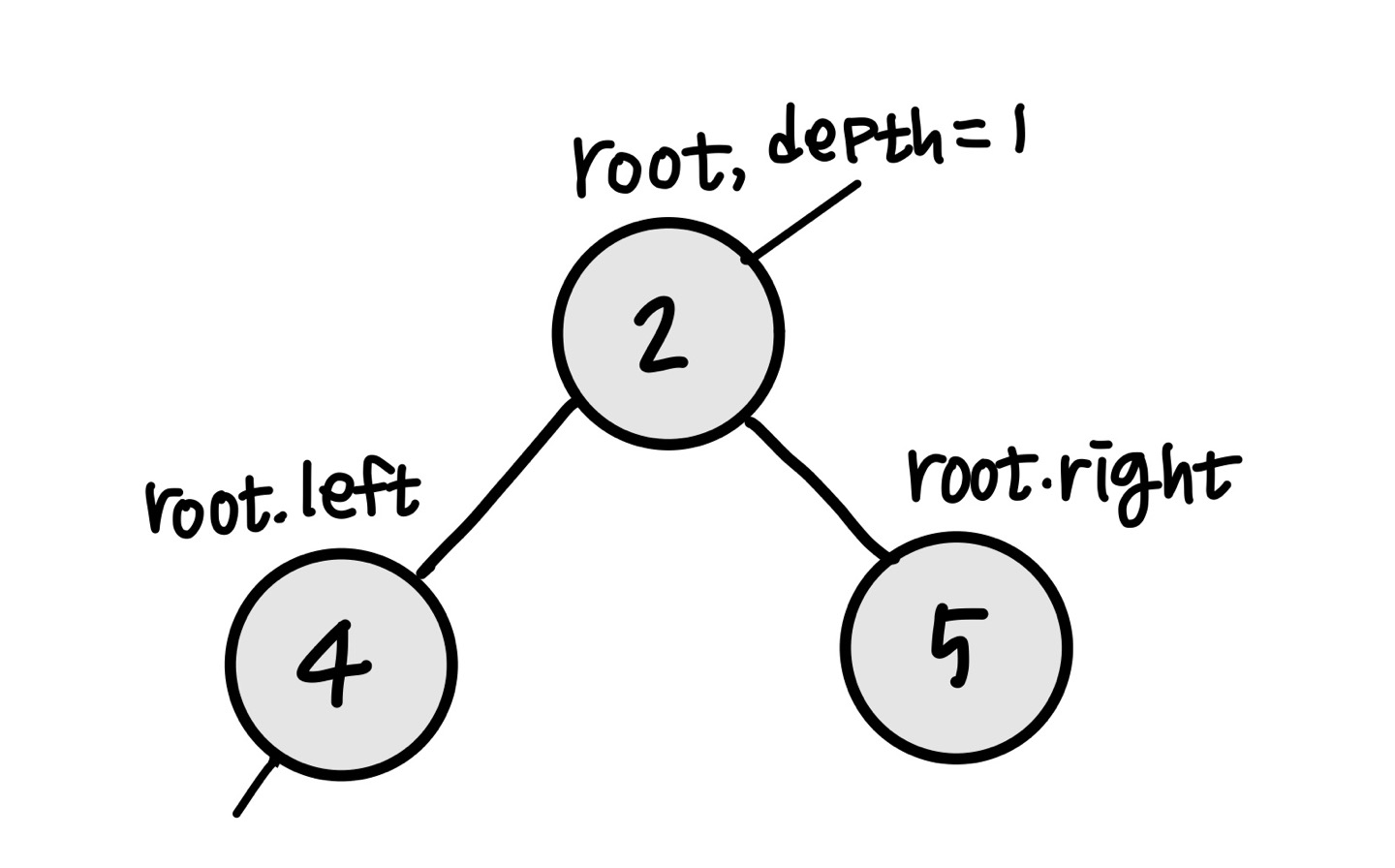
루트의 왼쪽 노드부터 재귀적으로 탐색한다. 다음 노드를 탐색할 때마다 depth를 1씩 증가시킨다.
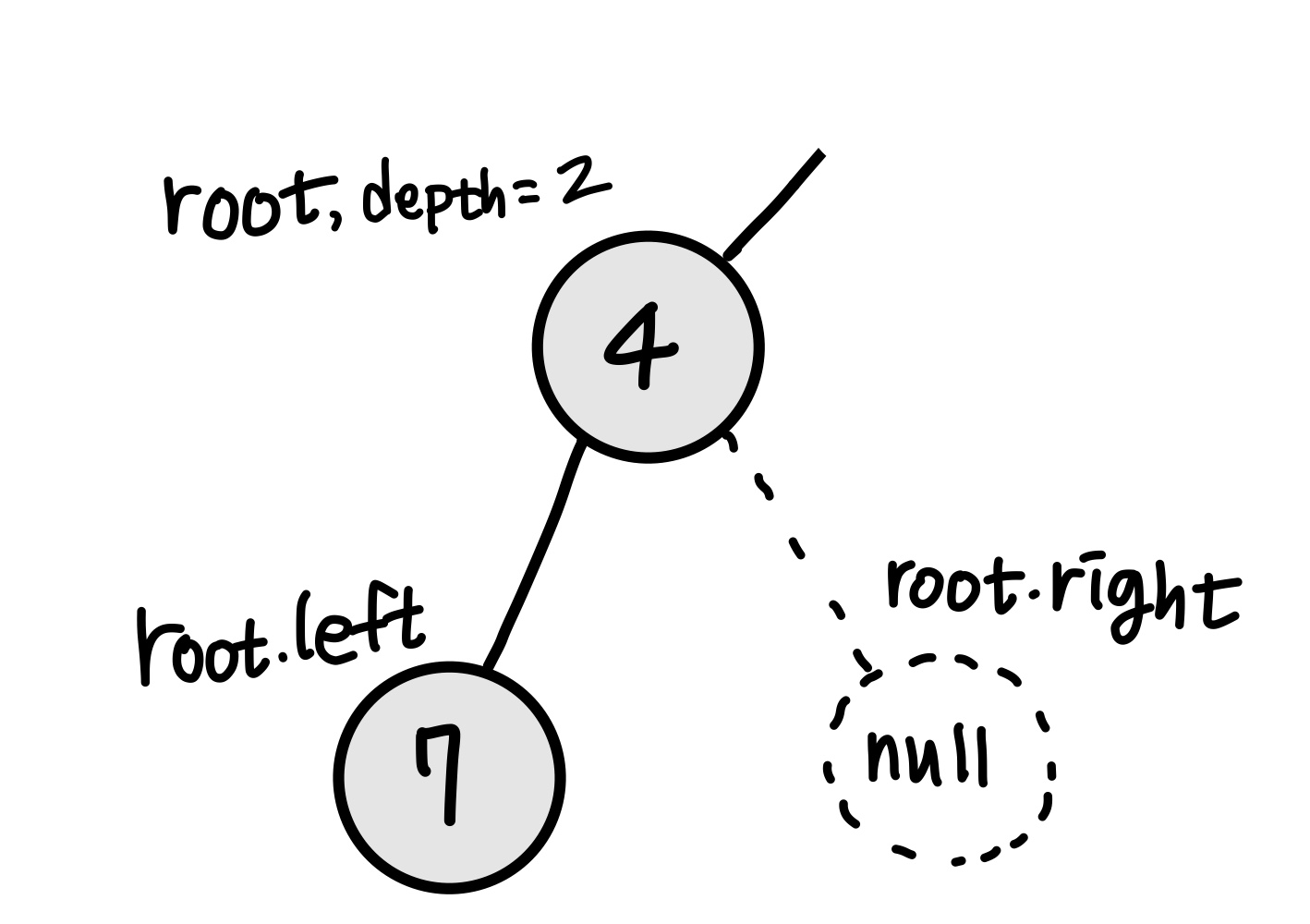
만약 탐색할 노드가 null인 경우 해당 노드의 탐색을 종료(return)한다.
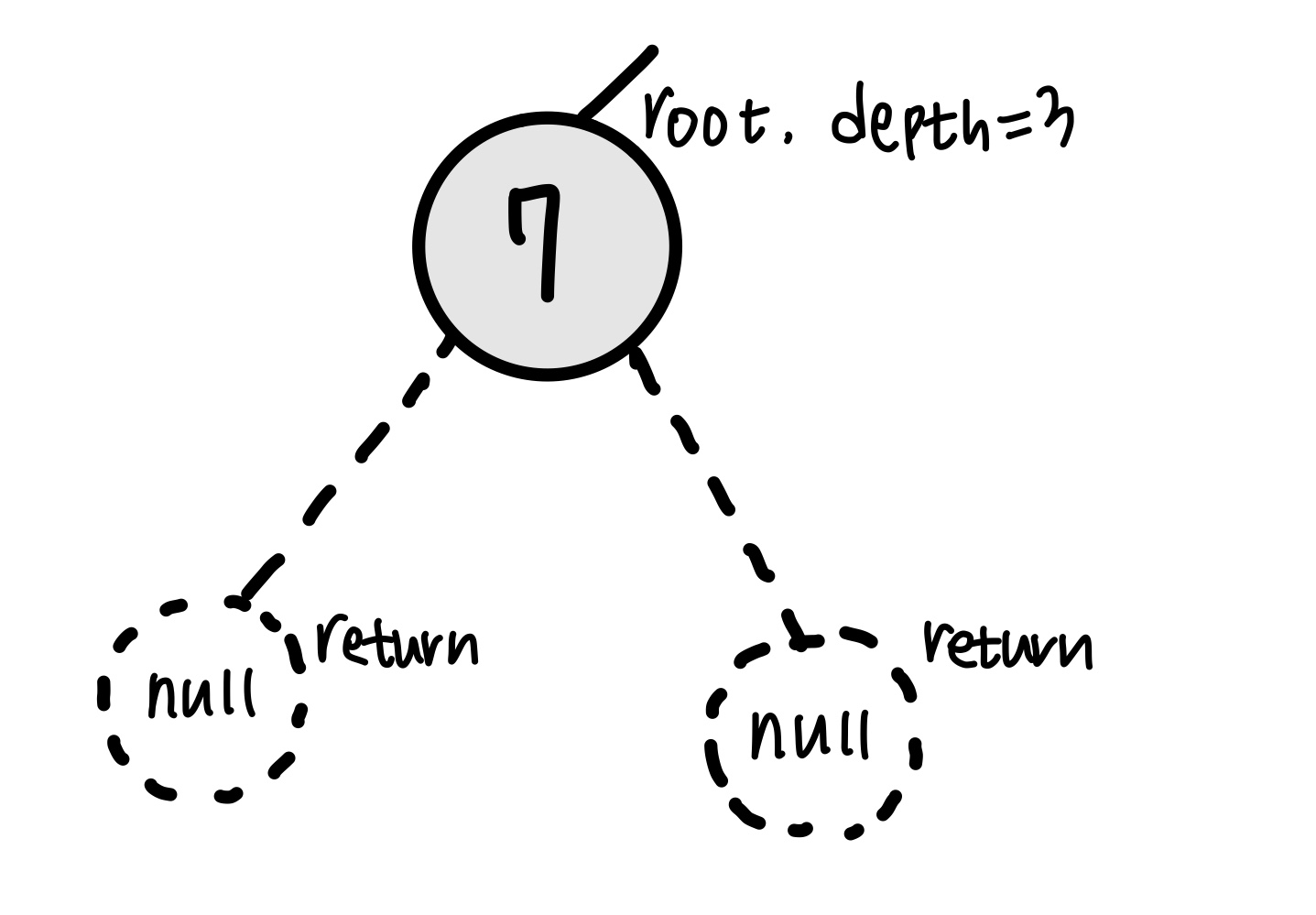
root 노드 왼쪽, 오른쪽 모두 null이므로 탐색을 종료한다. 가장 깊은 노드의 값인 7이 저장된다. 현재 가장 깊은 depth는 3이다.
이후에는 다시 4로 돌아가 4의 오른쪽 노드(null이기 때문에 return)를 탐색하고, 2로 돌아가 2의 오른쪽 노드 5을 탐색하게 된다.
BFS vs DFS
DFS를 사용하면 이진 트리의 모든 노드를 한 번씩 방문하게 되므로 시간 복잡도는 O(n)이다. 여기서 n은 트리의 노드 수를 의미한다.
BFS를 사용하여 문제를 해결하는 경우에도 모든 노드를 한 번씩 방문하게 되므로 시간 복잡도가 O(n)이다.
이 문제의 경우 BFS와 DFS 어느 쪽을 사용해도 해결할 수 있는데, 어떤 알고리즘을 사용해야 더 효율적일까?
좀 더 큰 예제를 만들어 살펴보자.
1
2
3
4
5
6
7
8
9
10
1
/ \
2 3
/ \ \
4 5 6
/ \ / \
7 8 9 10
/ \
11 12
BFS 탐색 시 큐의 변화
- 큐에 루트 노드(1)가 추가된다.
1
큐: [1]
- 큐에서 1을 꺼내고, 그 자식 노드인 2와 3을 큐에 추가한다.
1
큐: [2, 3]
- 큐에서 2를 꺼내고, 그 자식 노드인 4와 5를 큐에 추가한다.
1
큐: [3, 4, 5]
- 큐에서 3을 꺼내고, 그 자식 노드인 6을 큐에 추가한다.
1
큐: [4, 5, 6]
- 큐에서 4를 꺼내고, 그 자식 노드인 7과 8을 큐에 추가한다.
1
큐: [5, 6, 7, 8]
- 큐에서 5를 꺼내고, 그 자식 노드인 11과 12를 큐에 추가한다.
1
큐: [6, 7, 8, 11, 12]
- 큐에서 6을 꺼내고, 그 자식 노드인 9와 10을 큐에 추가한다.
1
큐: [7, 8, 11, 12, 9, 10]
- 큐에서 7을 꺼내고, 그 자식 노드가 없으므로 큐에 추가할 것이 없다.
1
큐: [8, 11, 12, 9, 10]
- 큐에서 8을 꺼내고, 그 자식 노드가 없으므로 큐에 추가할 것이 없다.
1
큐: [11, 12, 9, 10]
- 큐에서 11을 꺼내고, 그 자식 노드가 없으므로 큐에 추가할 것이 없다.
1
큐: [12, 9, 10]
- 큐에서 12를 꺼내고, 그 자식 노드가 없으므로 큐에 추가할 것이 없다.
1
큐: [9, 10]
- 큐에서 9를 꺼내고, 그 자식 노드가 없으므로 큐에 추가할 것이 없다.
1
큐: [10]
- 큐에서 10을 꺼내고, 그 자식 노드가 없으므로 큐에 추가할 것이 없다.
1
큐: []
DFS 탐색 시 스택의 변화
- 스택에 루트 노드(1)가 추가된다.
1
스택: [1]
- 스택에서 1을 꺼내고, 그 자식 노드인 2와 3을 스택에 추가한다.
1
스택: [2, 3]
- 스택에서 2를 꺼내고, 그 자식 노드인 4와 5를 스택에 추가한다.
1
스택: [3, 4, 5]
- 스택에서 4를 꺼내고, 그 자식 노드가 없으므로 스택에 추가할 것이 없다.
1
스택: [3, 5]
- 스택에서 5를 꺼내고, 그 자식 노드인 7을 스택에 추가한다.
1
스택: [3, 7]
- 스택에서 7을 꺼내고, 그 자식 노드가 없으므로 스택에 추가할 것이 없다.
1
스택: [3]
- 스택에서 3을 꺼내고, 그 자식 노드인 6을 스택에 추가한다.
1
스택: [6]
- 스택에서 6을 꺼내고, 그 자식 노드인 8을 스택에 추가한다.
1
스택: [8]
- 스택에서 8을 꺼내고, 그 자식 노드가 없으므로 스택에 추가할 것이 없다.
1
스택: []
DFS의 경우 한 경로를 따라 최대한 깊이 들어가므로 현재 경로에 있는 노드들만을 스택에 저장한다. 따라서 스택에 저장되는 노드의 수는 현재 경로의 길이와 비례한다.
어떤 것을 사용하면 좋을까?
주어진 트리의 깊이가 깊다면 BFS를 사용하는 것이 낫고, 너비가 넓다면 DFS를 사용하는 것이 공간 복잡도 측면에서 나을 것이다.
위 실행 과정을 살펴보면 BFS가 더 많은 공간을 차지하는 것처럼 보이지만, DFS를 사용했을 때 만약 트리의 깊이가 매우 깊다면 오히려 호출 스택의 깊이가 커져 스택 오버플로우를 유발할 수 있다.
이번 문제는 이진 트리로 루트 노드의 왼쪽, 오른쪽만을 너비로 가지므로 BFS가 더 적합해보인다.
최단 경로를 찾고 싶을 땐 BFS, 모든 가능한 후보를 탐색하면서 유효한 후보만을 골라낼 때에는 DFS를 사용하는 게 효율적인 것 같다.
정답 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class DeepestLeavesSum {
int deepestSum = 0;
int maxDepth = 0;
public int deepestLeavesSum(TreeNode root) {
dfs(root, 0);
return deepestSum;
}
private void dfs(TreeNode node, int depth) {
if (node == null) return;
if (depth > maxDepth) {
maxDepth = depth;
deepestSum = node.val;
} else if (depth == maxDepth) {
deepestSum += node.val;
}
dfs(node.left, depth + 1);
dfs(node.right, depth + 1);
}