[99클럽 코테 스터디 18일차 TIL] 동적 계획법으로 Count Square Submatrices with All Ones 풀이

문제

Leetcode - Square Submatrics with All Ones 문제를 보고 풀이한 내용이다.

Given a m * n matrix of ones and zeros, return how many square submatrices have all ones.

Example 1:

Input: matrix =

[
  [0,1,1,1],
  [1,1,1,1],
  [0,1,1,1]
]

Output: 15

Explanation:

There are 10 squares of side 1.

There are 4 squares of side 2.

There is 1 square of side 3.

Total number of squares = 10 + 4 + 1 = 15.

Example 2:

Input: matrix =

[
  [1,0,1],
  [1,1,0],
  [1,1,0]
]

Output: 7

Explanation:

There are 6 squares of side 1.

There is 1 square of side 2.

Total number of squares = 6 + 1 = 7.

풀이

정말 슬프게도 난 배열 문제에 너무너무 약하다. 공간지각능력 부족이 여기서도 영향을 끼치는 걸까😂 이번 Solution도 정답을 참고하고야 말았다. 대신 정답을 잘 이해하기 위해 그림을 그려 어떻게 풀 수 있는지 면밀하게 살펴보도록 노력했다.

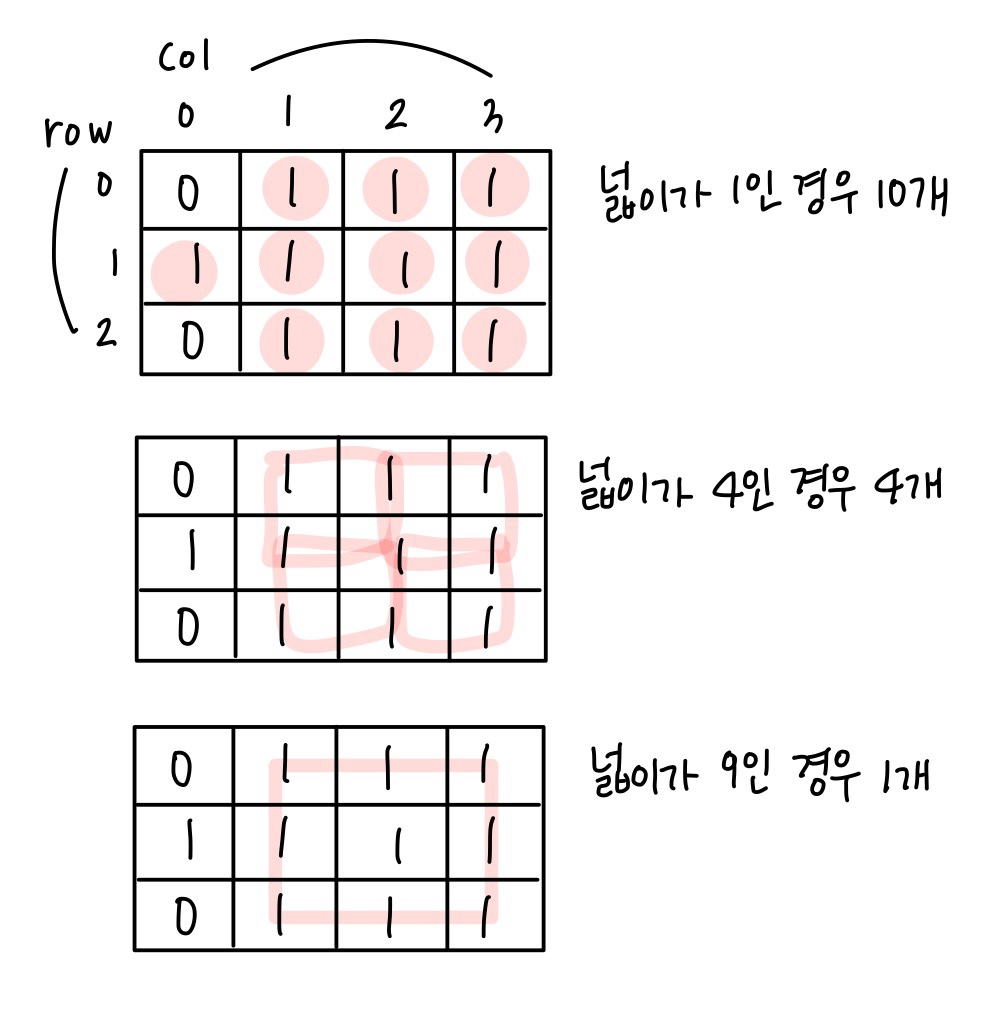
Example 1을 그림으로 나타냈다. 위 그림과 같이 넓이가 1인 작은 정사각형 10개, 넓이가 4인 정사각형 4개, 넓이가 9인 큰 정사각형 1개로 총 15개의 정사각형을 만들 수 있다.

눈으로 봤을 때는 딱 봐도 어떤 부분이 정사각형인지 알 수 있지만, 컴퓨터에게 이 사각형이 정사각형인지 어떻게 알려줄 수 있을까?

일단 넓이가 1인 정사각형의 경우 전체 배열을 순회하면서 현재 위치가 1이라면 정사각형 개수를 +1 해주면 된다.

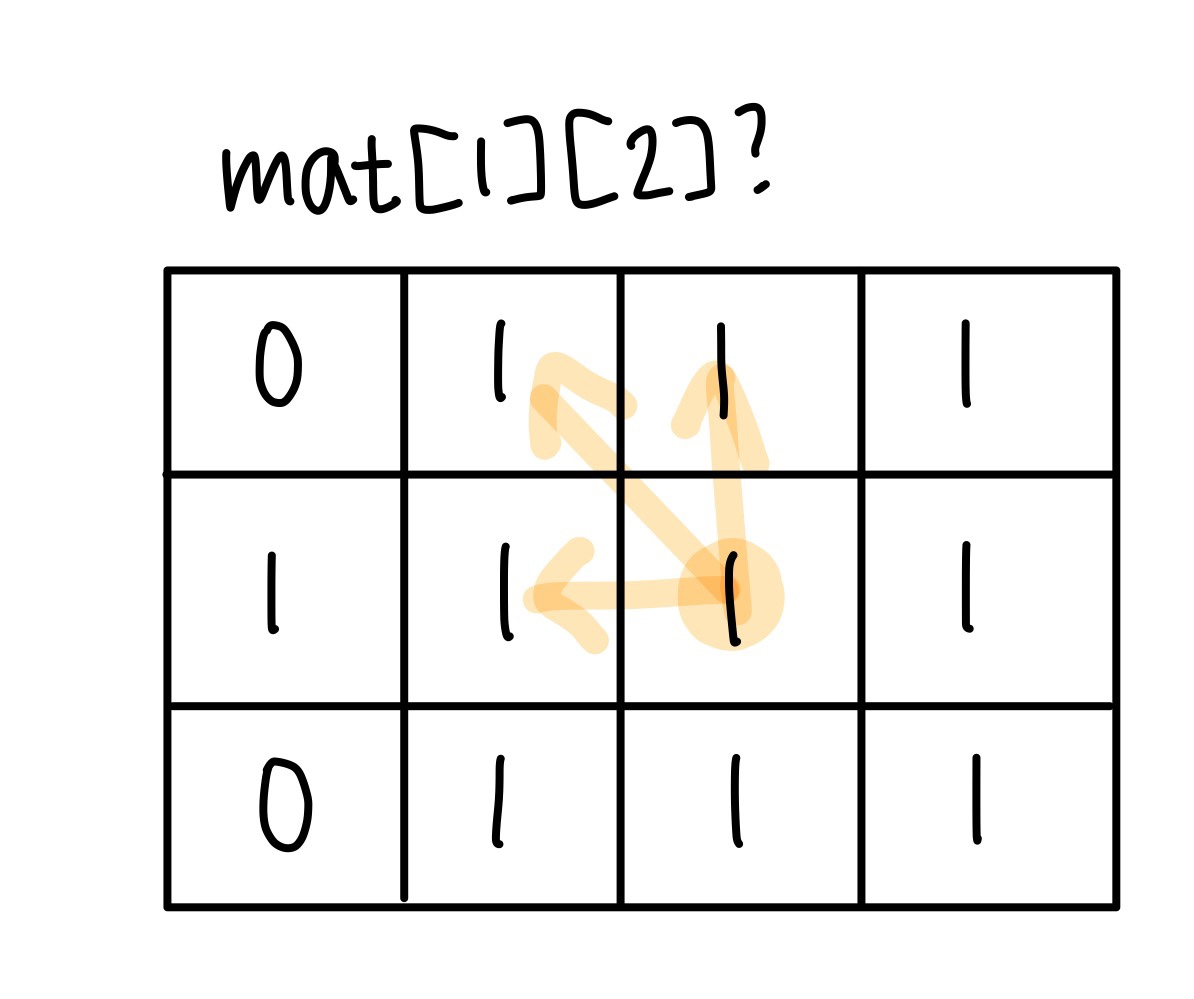
그럼 넓이가 4인 정사각형을 한 번 판별해보자.

넓이가 4인 정사각형은 위 그림과 같이 mat[1][2]에서 판별할 수 있다. 만약 현재 위치의 위(mat[row - 1][col]), 왼쪽(mat[row][col - 1]), 왼쪽 대각선 위(mat[row - 1][col - 1])가 1이라면 그 위치에 넓이 4짜리 정사각형이 한 개 있음을 알 수 있다.

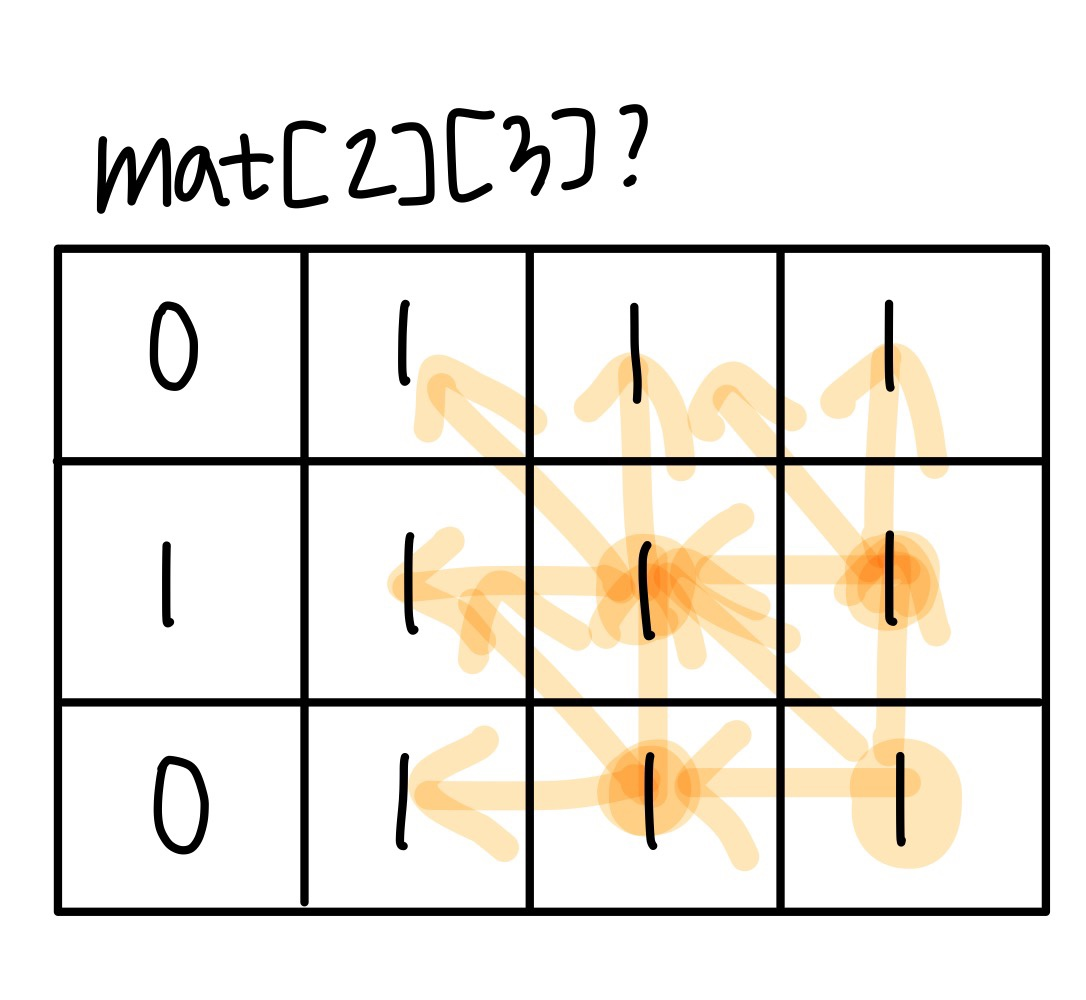
그렇다면 넓이가 9인 정사각형은 어떻게 알 수 있을까?

넓이가 9인 정사각형은 위 그림과 같이 mat[2][3]에서 판별할 수 있다. 넓이가 4인 정사각형을 판별할 때와 같이 위, 왼쪽, 왼쪽 대각선 위를 검사해본다. 그런데 각각의 위치에서 만들 수 있는 넓이 4짜리 정사각형이 하나씩 있다면 현재 위치에 넓이가 4인 정사각형과 넓이가 9인 정사각형이 한 개 있음을 알 수 있다.

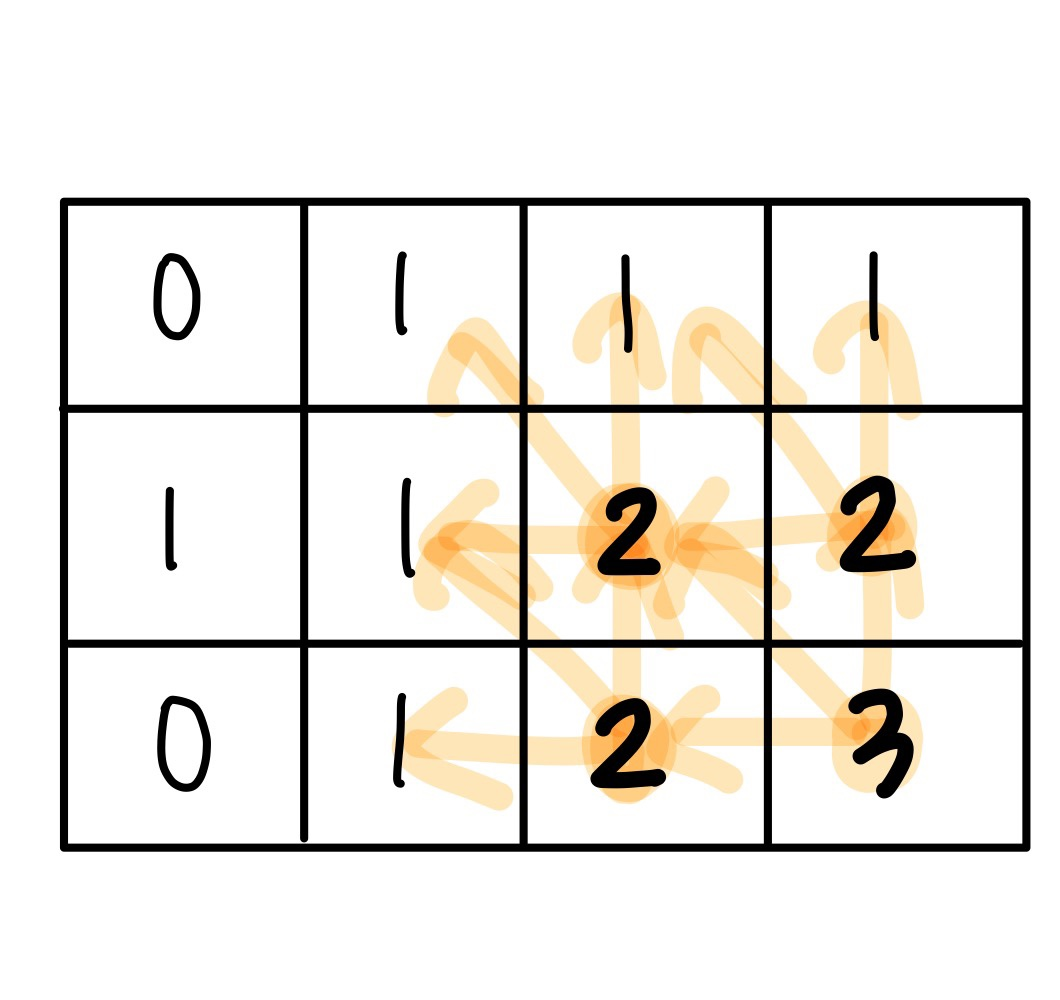
즉, 넓이가 4인 정사각형을 구한 결과를 가지고 넓이가 9인 정사각형의 개수를 구할 수 있다.

이렇게 작은 크기의 부분 문제들을 해결하고 이 값을 활용해 큰 문제를 해결할 수 있다면 Bottom-up Dynamic Programming 방식을 사용할 수 있다. 그러려면 부분 문제들의 결과를 저장해두었다가 사용해야 한다.

위와 같이 현재 위치에서 만들 수 있는 정사각형의 개수를 저장해두면, 그 결과를 사용해 더 큰 정사각형의 개수를 쉽게 구할 수 있게 된다.

따라서 필요한 로직은 다음과 같다.

* 만약 현재 위치가 0인 경우 정사각형을 만들 수 없으므로 검사하지 않고 다음 위치로 넘어간다.

* 만약 범위를 벗어난다면 넓이 4 이상의 정사각형을 만들 수 없다.

1. 현재 위치의 위를 검사한다.
2. 현재 위치의 왼쪽을 검사한다.
3. 현재 위치의 왼쪽 대각선 위를 검사한다.
4. 현재 위치는 위, 왼쪽, 왼쪽 대각선 위 검사 결과 만들 수 있는 가장 작은 개수의 정사각형이다. (모든 개수가 같지 않으면 정사각형을 만들 수 없다.)
5. 현재 위치에 만들 수 있는 정사각형 개수를 저장한다.
6. 만들 수 있는 전체 정사각형 개수에 현재 위치의 정사각형 개수를 더한다.

정답 코드

public class Solution {
    public int countSquares(int[][] mat) {
        int count = 0;

        for(int row = 0; row < mat.length; row++){
            for(int col = 0; col < mat[0].length; col++){
                if(mat[row][col] == 1){ // 현재 값이 1인 경우
                    int min = Integer.MAX_VALUE; // min 값 초기화

                    if(col - 1 >= 0) // 만약 현재 열 - 1이 0보다 크거나 같으면(범위를 벗어나지 않으면)
                        min = Math.min(mat[row][col - 1], min); // 같은 행의 이전 열 값과 min 값 중 더 작은 값을 채택
                    else min = 0; // 범위를 벗어나면 min은 0

                    if(row - 1 >= 0) // 만약 현재 행 - 1이 0보다 크거나 같으면(범위를 벗어나지 않으면)
                        min = Math.min(mat[row - 1][col], min); // 같은 열의 이전 행 값과 min 값 중 더 작은 값을 채택
                    else min = 0; // 범위를 벗어나면 min은 0

                    if(row - 1 >= 0 && col - 1 >= 0) // 만약 현재 행과 열 - 1이 범위를 벗어나지 않으면
                        min = Math.min(min, mat[row - 1][col - 1]); // 현재까지의 가장 작은 값과 왼쪽 위 대각선 값 비교
                    else min = 0; // 범위를 벗어나면 min은 0

                    mat[row][col] += min; // 현재 위치에 min 값을 더해줌
                    count += mat[row][col]; // count에 현재 위치 값을 더해줌(min이 0이여도 현재 위치가 1이면 정사각형)
                }
            }
        }
        return count;
    }
}