[99클럽 코테 스터디 16일차 TIL] 동적 계획법으로 Count Sorted Vowel Strings 풀이

문제

Leetcode - Count Sorted Vowel Strings 문제를 보고 풀이한 내용이다.

Given an integer n, return the number of strings of length n that consist only of vowels (a, e, i, o, u) and are lexicographically sorted.

A string s is lexicographically sorted if for all valid i, s[i] is the same as or comes before s[i+1] in the alphabet.

Example 1:

Input: n = 1 Output: 5 Explanation: The 5 sorted strings that consist of vowels only are [“a”,”e”,”i”,”o”,”u”].

Example 2:

Input: n = 2 Output: 15 Explanation: The 15 sorted strings that consist of vowels only are [“aa”,”ae”,”ai”,”ao”,”au”,”ee”,”ei”,”eo”,”eu”,”ii”,”io”,”iu”,”oo”,”ou”,”uu”]. Note that “ea” is not a valid string since ‘e’ comes after ‘a’ in the alphabet.

Example 3:

Input: n = 33 Output: 66045

Constraints: 1 <= n <= 50

풀이

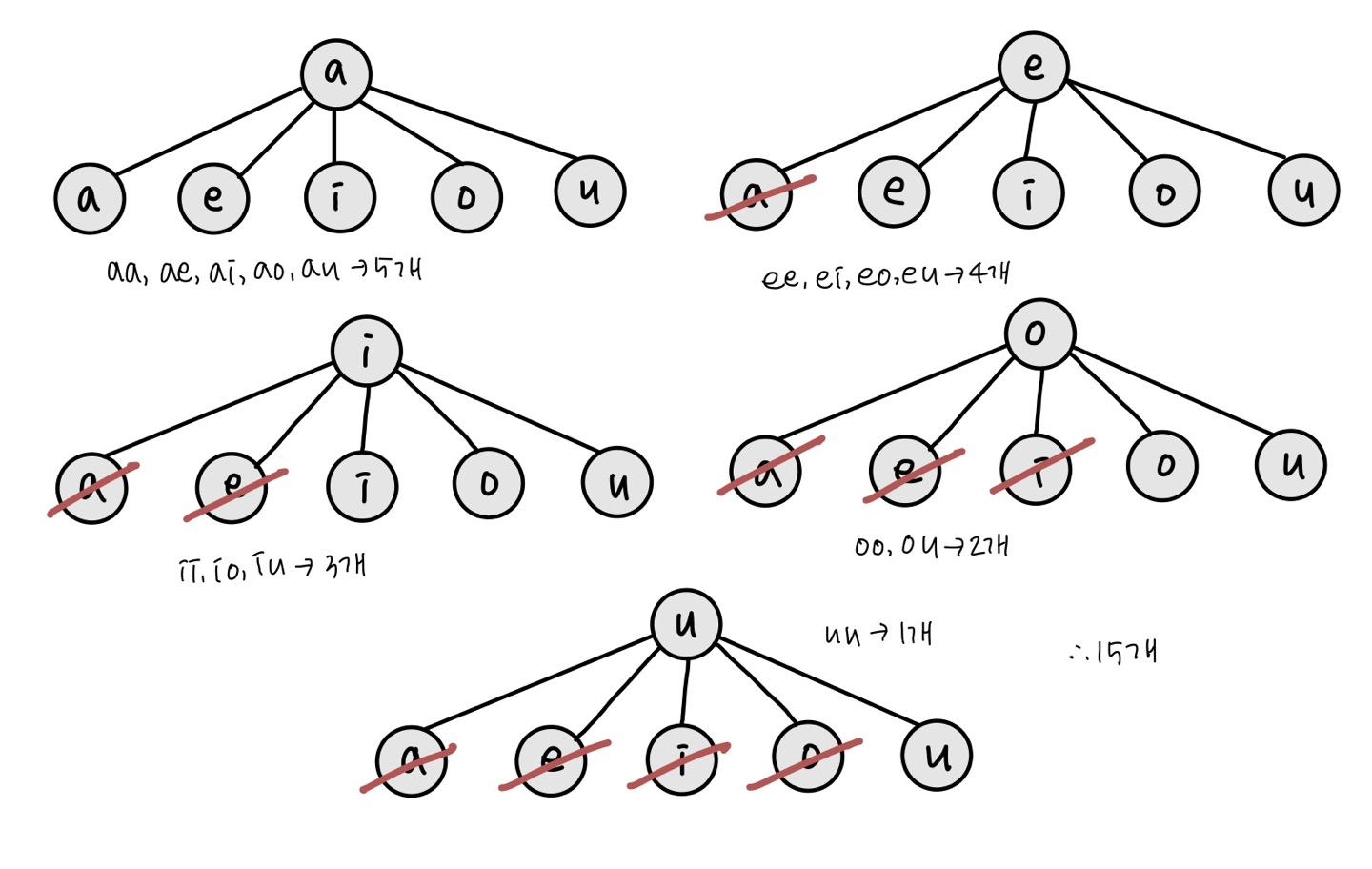
n = 2인 경우 가능한 문자열의 경우의 수를 트리 구조로 그려보자.

빨간색으로 빗금 쳐진 ea, ia, ie와 같은 노드들은 사전 순으로 정렬이라는 조건에 만족하지 못하는 노드들이다.

a는 5개의 노드, e는 4개의 노드, i는 3개의 노드, o는 2개의 노드, u는 1개의 노드를 가져 총 15개의 문자열을 만들 수 있음을 알 수 있다.

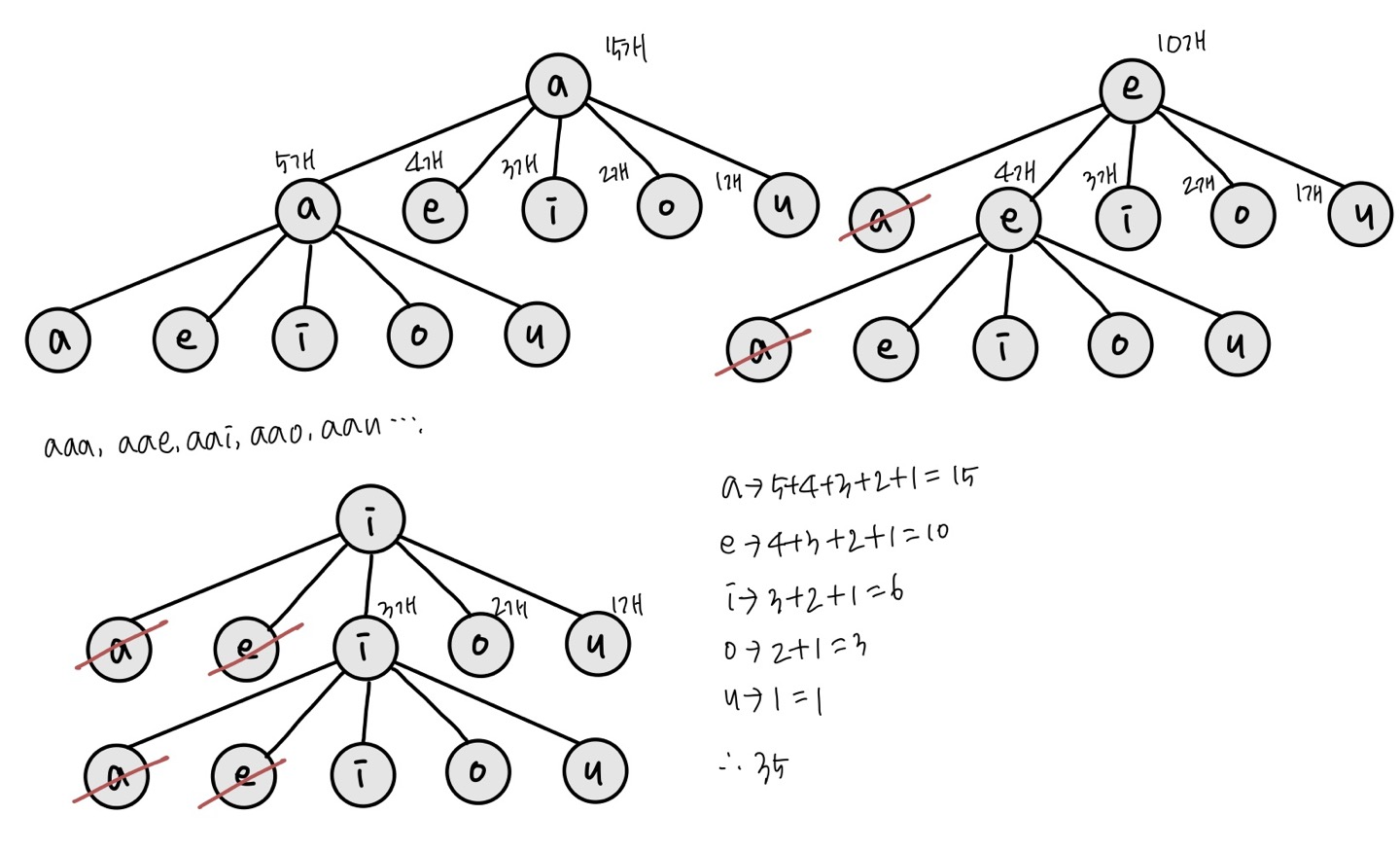
이번엔 n = 3인 경우의 트리 구조를 살펴보자.

a의 하위 노드 a는 다시 a, e, i, o, u를 하위 노드로 가진다. 따라서 a의 하위 노드 a는 5개의 문자열(aaa, aae,aai,aao,aau)을 만들 수 있다.

그림엔 생략되어 있지만 a의 하위 노드 e인 경우도 마찬가지다. aea의 경우 aae가 사전 순으로 더 앞서있기 때문에 조건에 일치하지 않아 제외된다. 따라서 n = 2 일 때 살펴봤던 그림과 동일하게 4개의 노드를 하위 노드로 가지게 된다.

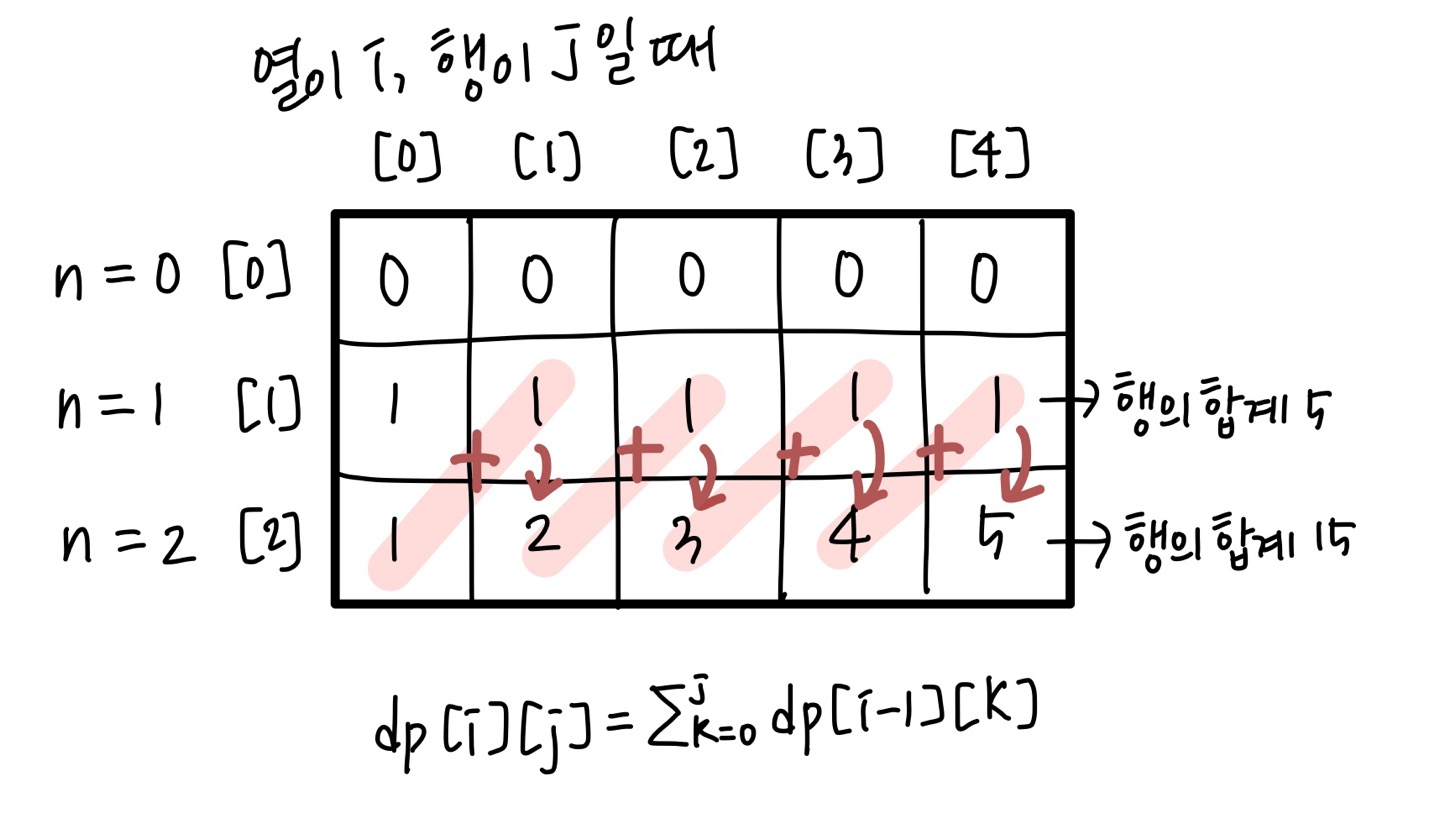
이 문제도 어제 풀었던 문제와 같이 작은 문제에서 구한 정답을 큰 문제에서 사용할 수 있기 때문에 점화식을 세워 풀어보았다.

예를 들어 n = 3이고 i로 만들 수 있는 문자열 개수를 알고 싶다면, 이전 값(n = 3일 때 e로 만들 수 있는 문자열 개수)에 n = 2일 때 i로 만들 수 있는 문자열 개수를 더해주면 된다.

정답 코드

public int countVowelStrings(int n) {
        // memorize list
        int[][] dp = new int[n + 1][5];

        // 초기화: 길이가 1인 문자열의 개수
        // dp 초기값 -> [[0, 0, 0, 0, 0], [1, 1, 1, 1, 1]]]
        for (int i = 0; i < 5; i++) {
            dp[1][i] = 1;
        }

        for (int i = 2; i <= n; i++) {
            for (int j = 0; j < 5; j++) {
                for (int k = 0; k <= j; k++) {
                    dp[i][j] += dp[i - 1][k];
                }
            }
        }

        int result = 0;
        for (int i = 0; i < 5; i++) {
            result += dp[n][i];
        }
        return result;
    }